Introducetion: 数据挖掘:k-means聚类介绍
Topic: Data Mining
URL: https://dl.acm.org/doi/abs/10.1145/1014052.1014118
Where: KDD
Year: 2004
本文只是学习并记录笔记,如有错误或不足请谅解指正,谢谢!
前提知识
k-means(K均值)
是基于数据划分的无监督聚类算法
聚类算法:可以理解为无监督的分类方法
- 基本原理
- 对于基于划分的这一类聚类算法而言,其方法是将样本的矢量空间划分为多个区域 $
{{S_i|^k_{i=1}}}$,每个区域都存在一个区域中心$C_i|^k_{i=1}$,这样对于每一个样本,都可以建立一种样本到区域中心的映射: $q(x)=\sum^k_{i=1}1(x{\in}S_i)C_i$其中1()为指示函数,即代表样本x是否属于区域S - 不同的基于划分的聚类算法的主要区别就在于如何建立相应的映射方式
q(x),在k-means中,映射是通过样本与各中心之间的误差平方和最小这一准则来建立的
- 对于基于划分的这一类聚类算法而言,其方法是将样本的矢量空间划分为多个区域 $
- 主要实现步骤:
- 初始化聚类中心$
C_1^{(0)}, C_2^{(0)} ,C_3^{(0)}$ …… $C_k^{(0)}$可选取前K个样本或者随机选取K个样本 - 分配各个样本$
x_j$到距离最相近的聚类集合,样本分配依据为:$S_i^{(t)}=\{x_j\mid\|{x_j-c_j^{(t)}\|_2^2}\leq\|x_j-c_p^{(t)}\|_2^2\}$其中i=1,2,…,k,p≠j - 根据上一步的分配结果,更新聚类中心:$c_i^{(t+1)}=\dfrac{1}{|S_i^{(t)}|}\sum_{x_j\in{S_i^{(t)}}}x_j$
- 若迭代次数达到最大迭代步数或者前后两次迭代的差小于设定阈值ε
,即$\|c_i^{(t+1)}-c_i^{(t)}\|_2^2<\varepsilon$,则算法结束,否则重复步骤2
- 初始化聚类中心$

计算每个样本点簇中心的距离,然后判断出到哪个簇中心距离最短,然后分给那个簇。然后下次迭代时,簇中心就按照新分配的点重新进行计算了,然后所有的点再同样计算样本点到簇中心的距离,重新分配到不同的簇中。所以这样不断迭代下去,就能够收敛了,得到最后的聚类效果。
问题:对于非标准正态分布和非均匀分布的样本,k-means聚类效果不好,其主要原因是k-means是假设相似度可以用二次欧式距离等价的衡量,但是在实际的样本集合中这个假设不一定实用。
为了克服这个局限性,k-means需要推广到更广义的度量空间,其两种经典的改进框架如下:
Kernel k-means(核k-means方法)
将样本点$x_i$通过某种映射方式$x_i\rightarrow \phi(x_i)$,映射到新的高维空间Φ
,在该空间中样本点之间的内积可以通过对应的核函数进行计算,即:
$k(x_i,x_j)=\phi(x_i)^T\phi(x_j)$
借助核函数,可以在新的空间进行k-means聚类,而此时样本之间的相似度取决于核函数的选择。
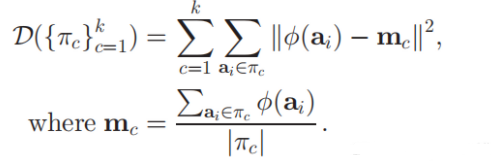
ai表示样本点,mc表示每个簇的质心。
$\phi()$表示将样本点映射至高维空间。但这个函数是很难算出来的,因为这种非线性的函数映射,很难去得到准确的函数算法。且,簇的中心mc也很难去描述出来。
因此需要对这个函数进行改造:
将
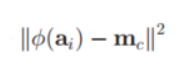
改为
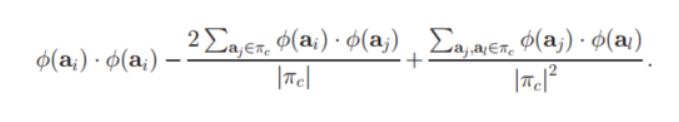
即:将该公式展开。
我们可以发现:每一项中,需要使用到高维特征空间的值,都是在进行内积运算。因此符合我们之前所提到的,使用一个矩阵K函数,来代表高维特征空间中这两个值的内积结果。
即:$k(a_i,b_j)=\phi(a_i).\phi(b_j)$
所以,我们只需要得到一个K矩阵,矩阵中每个元素都表示高维空间,这两个样本点映射成特征后,进行内积计算所得到的结果。所以这个矩阵,实际上就是一个核函数矩阵。
weighted kernel k-means
在kernel k-means基础上,为每一个样本点给出一个权重,以区分不同样本点的重要性。

公式中计算样本高维空间特征到簇中心距离 的平方后,还乘以了一个权重$w_j$
Spectral Clustering(谱聚类方法)
它的主要思想是把所有的数据看做空间中的点,这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,通过对所有数据点组成的图进行切图,让切图后不同的子图间边权重和尽可能的低,而子图内的边权重和尽可能的高,从而达到聚类的目的。
摘要与背景
Kernel k-means和谱聚类都被用于识别在输入空间中非线性可分离的聚类。尽管进行了大量的研究,但这些方法仍然只是松散地联系在一起。
本文中,作者给出了它们之间明确的理论联系。证明了Weighted kernel k-means目标函数的通用性,并推导出归一化切割的谱聚类目标作为一种特殊情况。
提出了一种新的Weighted kernel k-means算法(前提给出正定相似矩阵),其单调地减少了归一化割。
意义:
- 基于特征向量的算法(可能在计算上是禁止的)对于最小化规范化切割不是必需的
- 各种技术,例如局部搜索和加速方案,可以用来提高核k-均值的质量和速度
背景:
- 聚类是数据挖掘的重要问题,k-means是最流行的聚类算法之一,受到了相关研究者的广泛关注。
- k-means的一个主要缺点是,它不能分离在输入空间中非线性可分离的簇。当时的两种解决方法是:①Kernel k-means,在聚类之前,使用非线性函数将点映射到高维特征空间,然后Kernel k-means在新空间中用线性分隔符对点进行分割。②spectral clustering algorithms(谱聚类算法),使用亲和矩阵的特征向量来获得数据的聚类。谱聚类中常用的目标函数是最小化归一化切割的
从表面上看,Kernel k-means和谱聚类似乎是完全不同的方法。
本文的目的:证明Kernel k-means和谱聚类之间的相关性(可以将加权核k-means目标函数重写为迹最大化问题)。这样当遇到需要计算大量特征向量的情景时,可以使用类似k-means的迭代算法来完成最小化图的归一划分。
方法
- 常见的非线性核函数

Weighted Kernel k-means
k-means聚类算法可以通过使用核函数来增强;通过使用从原始(输入)空间到高维特征空间的适当非线性映射,可以提取在输入空间中非线性可分离的聚类。
此外,我们可以通过为每个点a引入一个权值来推广核k-means算法,用w(a)表示。
算法:

第二项每个数据点计算一次,每次计算的成本是O(n),导致每次迭代的成本是O(n2)。
因此,每次迭代的复杂度为O(n2)标量操作。首先,我们必须计算核矩阵K,这通常需要时间O(n2m),其中m是原始点的维数。若总迭代次数为τ,则算法1的时间复杂度为O(n2(τ + m))。
Spectral clustering(谱聚类)
基本思想是利用样本数据的相似矩阵(拉普拉斯矩阵)进行特征划分后得到的特征向量进行聚类。
作者在本文重点研究归一化划分谱算法(normalized cut spectral algorithm)。
这里作者主要对另一篇论文(Multiclass spectral clustering)进行简单描述,将归一化划分准则等价于下列
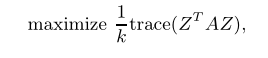
其中
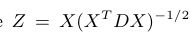
X是一个用于划分的n×k指示器矩阵
THE SPECTRAL CONNECTION
乍一看,Weighted Kernel k-means和使用谱聚类的归一化切割似乎有很大的不同。毕竟,谱聚类使用特征向量来帮助确定分区,而特征向量没有出现在核k-means中。
然而,我们看到归一化切割问题可以表示为一个轨迹最大化(trace maximization)问题,在这一节中,我们展示了如何将Weighted Kernelk-means也表示为一个轨迹最大化问题。这将展示如何连接这两种聚类方法。
首先对πj 进行一个变形:
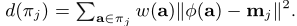
$π_j$表示集群(簇)
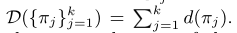
之后定义:
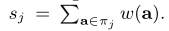
其中$s_j$表示$π_j$的权重之和
$W$是所有点$w_i$权重的对角矩阵,$W_j$是$π_j$中权重的对角矩阵。
将均值向量$m_j$改为:
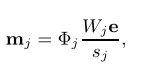
其中,W是所有点wi权重的对角矩阵,Wj是πj中权重的对角矩阵,Φj是与簇$π_j$相关的点矩阵,e是所有大小合适的向量
通过上述公式,可以将$π_j$的变形改为:
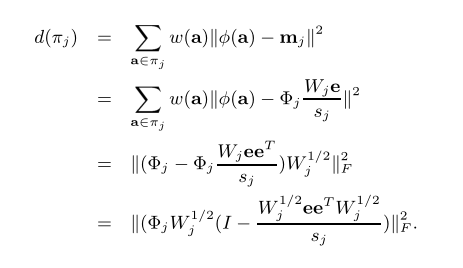
由于:
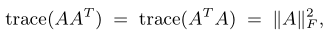
且:
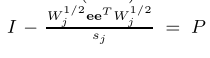
是一个正交的投影,P$^2$=P,因为
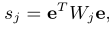
因此又可以得到:
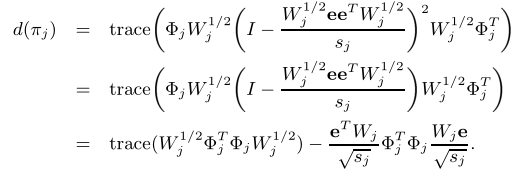
如果将点的完整矩阵表示为Φ=[Φ1,Φ2,…,Φk],那么就得到:

Y是一个n×k的正交矩阵,即Y $^T$Y = I
由于trace($ΦWΦ^T$)是一个常数,所以我们加权核k-means的目标函数((1)中目标函数的最小化)等价于trace($Y^T W ^1/2Φ^TΦW^1/2Y$)的最大化,其中$Φ^TΦ$就是数据的核矩阵K,因此可以化为trace($Y^T W ^1/2KW^1/2Y$)
IMPLICATIONS
Normalized Cuts using Weighted Kernel k-means
使用加权核k均值的归一化切割
Kernel k-means using Eigenvectors
使用特征向量的核k均值
Interpreting NJW As Kernel k-means
将NJW解释为核k-means
EXPERIMENTAL RESULTS
首先用2度多项式核k均值说明基因的“直径聚类”
证明了用特征向量初始化核k-means可以得到更好的初始和最终目标函数值和更好的聚类结果。因此,谱聚类与核kmeans之间的理论联系有助于获得更高质量的结果。
最后,我们展示了我们的距离估计技术节省了大量的计算时间,验证了我们的方法的可扩展性。
数据集
- Rosetta Inpharmatics的酵母数据集在300种条件下有5246个基因。
- UCI机器学习库(ftp://ftp.ics.uci.edu/ pub/machine-learningdatabases/ Pendigits)下载,该库包含手写数字的(x, y)坐标。该数据集包含7494个训练数字和3498个测试数字。每个数字都表示为16维空间中的一个向量。
结果
- We first illustrate “diametric clustering” of genes with degree2 polynomial kernel k-means.
首先用2度多项式kernel k-means证明了基因的“相反聚类” - with the handwriting recognition data set, we show that using eigenvectors to initialize kernel k-means gives better initial and final objective function values and better clustering results.
利用手写识别数据集,证明了用特征向量初始化kernel k-means可以得到更好的初始和最终目标函数值以及更好的聚类结果。 - 谱聚类与kernel kmeans之间的理论联系有助于获得更高质量的结果。
- 最后,作者展示了距离估计技术节省了大量的计算时间,验证了方法的可扩展性
Diametrical Clustering of Gene Expression Data(基因表达数据的聚类):
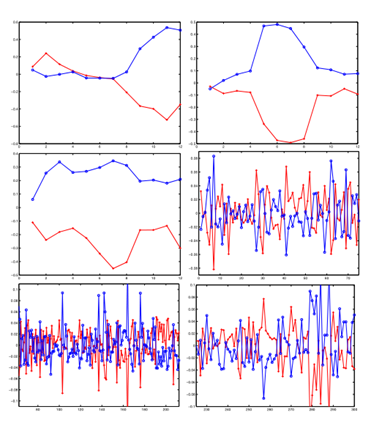
- 在基因表达聚类中,识别基因之间的反相关关系是很重要的,因为已经观察到,表达模式强烈反相关的基因也可能在功能上相似。
- 结果:2次多项式kernel k-means捕获了与相反聚类算法捕获的反相关。与论文“Diametrical clustering for identifying anti-correlated gene clusters”结果一致
Clustering Handwriting Recognition Data Set(聚类笔迹识别数据集)
使用谱聚类的初始化kernel k-means输出通常可以产生比纯随机初始化更好的聚类结果。
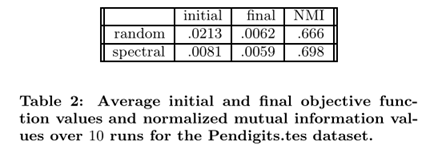
NMI值越高,表示聚类和真实类标签匹配越好
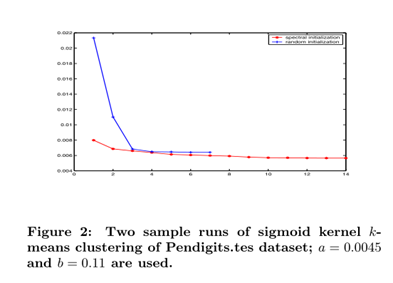
同时,作者还提出了“三角不等式估计”(triangle inequality estimation mentioned)的方法,以此计算距离
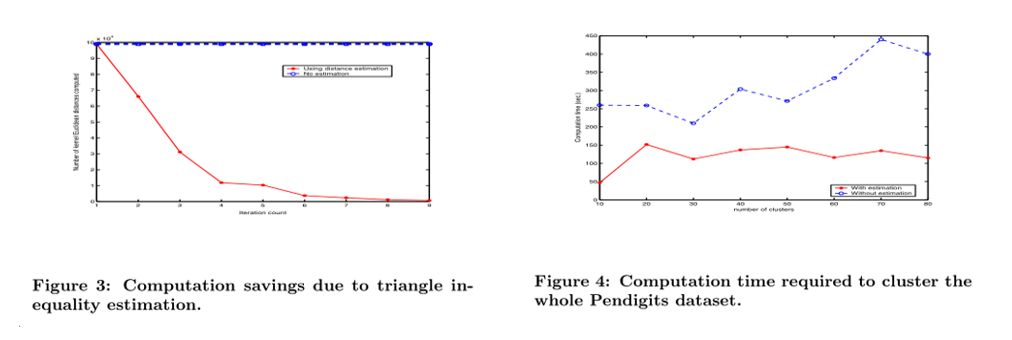
Conclusion
论文总结了传统的核k-means方法和谱聚类的方法,这两种方法看似是不相关的,但其实通过一定的公式推导和理论的证明,可以得到核k-means的方法也可以表达成为谱聚类那样的最大化迹的形式。
证明了weighted kernel k-means公式是非常通用的,并且归一化切割目标可以重铸为weighted kernel k-means 目标函数的一个特例。
